Ramification group
In number theory, more specifically in local class field theory, the ramification groups are a filtration of the Galois group of a local field extension, which gives a precisely information on the ramification phenomenon of the extension.
Ramification groups in lower numbering
Let 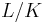 be a finite Galois extension of local fields with group
be a finite Galois extension of local fields with group  and finite residue fields
and finite residue fields 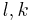 . We shall write
. We shall write 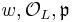 for the valuation, the ring of integers and its maximal ideal for
for the valuation, the ring of integers and its maximal ideal for  . It is known that one can write
. It is known that one can write ![\mathcal O_L = \mathcal O_K[\alpha]](/2012-wikipedia_en_all_nopic_01_2012/I/a981b4a66d1de2605fd5cacd4c201970.png) for some
for some 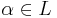 where
where 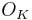 is the ring of integers of
is the ring of integers of  . (This is stronger than the primitive element theorem and is a consequence of Hensel's lemma.) Then, for each integer
. (This is stronger than the primitive element theorem and is a consequence of Hensel's lemma.) Then, for each integer 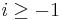 , we define
, we define 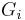 to be the set of all
to be the set of all 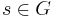 that satisfies the following equivalent conditions.
that satisfies the following equivalent conditions.
- (i)
 operates trivially on
operates trivially on 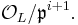
- (ii)
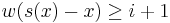 for all
for all 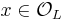
- (iii)
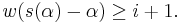
(i) shows that 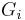 are normal and (ii) shows that
are normal and (ii) shows that 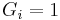 for sufficiently large
for sufficiently large  .
. 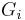 is then called the
is then called the  -th ramification group, and they form a finite decreasing filtration of
-th ramification group, and they form a finite decreasing filtration of  with
with 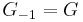 .
. 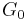 is called the inertia subgroup of
is called the inertia subgroup of  . Note:
. Note:
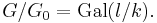 [1]
[1]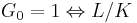 unramified.
unramified.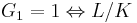 tamely ramified (i.e., the ramification index is prime to the residue characteristic.)
tamely ramified (i.e., the ramification index is prime to the residue characteristic.)
The study of ramification groups reduces to the totally ramified case since one has 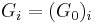 for
for 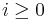 .
.
One also defines the function 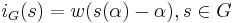 . (ii) in the above shows
. (ii) in the above shows 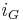 is independent of choice of
is independent of choice of  and, moreover, the study of the filtration
and, moreover, the study of the filtration 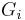 is essentially equivalent to that of
is essentially equivalent to that of 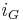 .[2]
.[2] 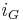 satisfies the following: for
satisfies the following: for 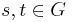 ,
,
Fix a uniformizer  of
of  .
. 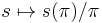 then induces the injection
then induces the injection 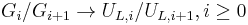 where
where 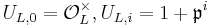 . It follows from this[3]
. It follows from this[3]
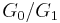 is cyclic of order prime to
is cyclic of order prime to 
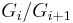 is a product of cyclic groups of order
is a product of cyclic groups of order  .
.
In particular, 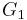 is a p-group and
is a p-group and  is solvable.
is solvable.
The ramification groups can be used to compute the different 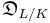 of the extension
of the extension 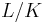 and that of subextensions:
and that of subextensions:
If  is a normal subgroup of
is a normal subgroup of  , then, for
, then, for 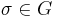 ,
, 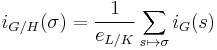 .[4]
.[4]
Combing this with the above one obtains: for a subextension 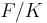 corresponding to
corresponding to  ,
,
If 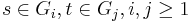 , then
, then 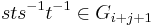 .[6] In the terminology of Lazard, this can be understood to mean the Lie algebra
.[6] In the terminology of Lazard, this can be understood to mean the Lie algebra 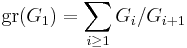 is abelian.
is abelian.
Ramification groups in upper numbering
If  is a real number
is a real number 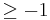 , let
, let 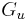 denote
denote 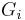 where i the least integer
where i the least integer 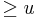 . In other words,
. In other words, 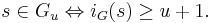 Define
Define  by
by
where, by convention, 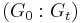 is equal to
is equal to 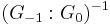 if
if 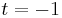 and is equal to
and is equal to 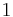 for
for 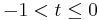 . Then
. Then 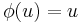 for
for 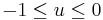 . It is immediate that
. It is immediate that  is continuous and strictly increasing, and thus has the continuous inverse function
is continuous and strictly increasing, and thus has the continuous inverse function  defined on
defined on 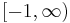 . Define
. Define 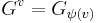 .
. 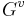 is then called the v-th ramification group in upper numbering. In other words,
is then called the v-th ramification group in upper numbering. In other words, 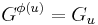 . Note
. Note 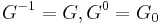 . The upper numbering is defined so as to be compatible with passage to quotients: if
. The upper numbering is defined so as to be compatible with passage to quotients: if  is normal in
is normal in  , then
, then
 for all
for all 
(whereas lower numbering is compatible with passage to subgroups.)
Herbrand's theorem states that  for
for 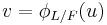 where
where 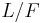 is a subextension corresponding to
is a subextension corresponding to  .
.
The upper numbering for an abelian extension is important because of the Hasse–Arf theorem. It states that if  is abelian, then the jumps in the filtration
is abelian, then the jumps in the filtration 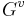 are integers; i.e.,
are integers; i.e., 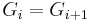 whenever
whenever 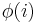 is not an integer.
is not an integer.
References
- (1980), Local Fields, Berlin, New York: Springer-Verlag, ISBN 9780387904245, MR0554237
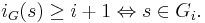
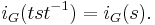
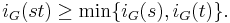
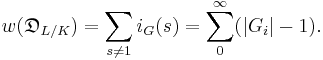
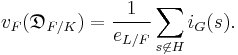
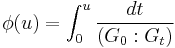
 is canonically isomorphic to the decomposition group.
is canonically isomorphic to the decomposition group.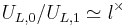 and
and